Create Creates a new instance of the default implementation of the Elliptic Curve Digital Signature Algorithm (ECDSA). Create(ECCurve) Creates a new instance of the default implementation of the Elliptic Curve Digital Signature Algorithm (ECDSA) with a newly generated key over the specified curve. Because the Generator point changes for each handshake, the public key must not be generator beforehand. If this is the case, then what is the purpose of ever generating an ECC public key? For a project I am working on, it is necessary to generate a public key to be placed in a certificate signing request to connect with AWS.

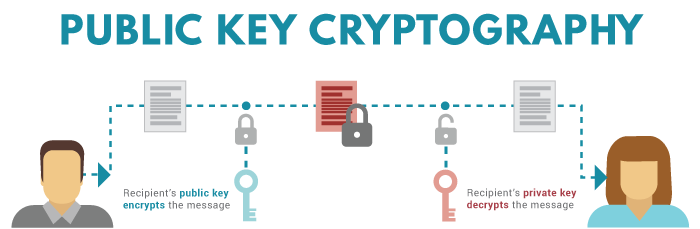
• Apr 13, 2020  While each private key is used to derive precisely one public key, it is impossible to determine the private key from knowledge of the public key. With older asymmetric encryption techniques like Diffie-Hellman key exchange, the public keys are exchanged between two individuals and used to derive a shared private key.
• The -y option will read a private SSH key file and prints an SSH public key to stdout. The public key part is redirected to the file with the same name as the private key but with the.pub file extension. If the key has a password set, the password will be required to generate the public key. To check the details of the generated public key.
• Jul 16, 2018 creating a public key with ECDSA; encrypting the key with SHA-256 and RIPEMD-160; calculating the checksum with double SHA-256; encoding the key with Base58. Depending on the form of public key (full or compressed), we get different addresses, but both are perfectly valid. Here’s the full algorithm for the uncompressed public key.
• Oct 24, 2013  Computing the private key from the public key in this kind of cryptosystem is called the elliptic curve discrete logarithm function. This turns out to be the Trapdoor Function we were looking for. What does it all mean? The elliptic curve discrete logarithm is the hard problem underpinning elliptic curve cryptography.

-->

Definition

Creates a new instance of an implementation of the Elliptic Curve Digital Signature Algorithm (ECDSA).

Overloads

Create()	Creates a new instance of the default implementation of the Elliptic Curve Digital Signature Algorithm (ECDSA).
Create(ECCurve)	Creates a new instance of the default implementation of the Elliptic Curve Digital Signature Algorithm (ECDSA) with a newly generated key over the specified curve.
Create(ECParameters)	Creates a new instance of the default implementation of the Elliptic Curve Digital Signature Algorithm (ECDSA) using the specified parameters as the key.
Create(String)	Creates a new instance of the specified implementation of the Elliptic Curve Digital Signature Algorithm (ECDSA).

Creates a new instance of the default implementation of the Elliptic Curve Digital Signature Algorithm (ECDSA).

Returns

A new instance of the default implementation (ECDsaCng) of this class.

Creates a new instance of the default implementation of the Elliptic Curve Digital Signature Algorithm (ECDSA) with a newly generated key over the specified curve.

Parameters

Returns

A new instance of the default implementation (ECDsaCng) of this class.

See also

Creates a new instance of the default implementation of the Elliptic Curve Digital Signature Algorithm (ECDSA) using the specified parameters as the key.

Parameters

parameters

ECParameters

The parameters representing the key to use.

Returns

A new instance of the default implementation (ECDsaCng) of this class.

See also

Creates a new instance of the specified implementation of the Elliptic Curve Digital Signature Algorithm (ECDSA).

Parameters

algorithm

String

The name of an ECDSA implementation. The following strings all refer to the same implementation, which is the only implementation currently supported in the .NET Framework:

• 'ECDsa'

• 'ECDsaCng'

• 'System.Security.Cryptography.ECDsaCng'

https://Tomtom-Mydrive-Connect-Download-Mac.peatix.com/. You can also provide the name of a custom ECDSA implementation.

Returns

A new instance of the specified implementation of this class. If the specified algorithm name does not map to an ECDSA implementation, this method returns null.

Exceptions

The algorithm parameter is null.

Remarks

If you develop your own implementation of an ECDsa object, you can use the Create(String) method overload to create a custom algorithm string that specifies your implementation.

If you specify a custom value for the algorithm parameter, the CryptoConfig object will use it to determine whether an ECDSA object can be created.

Applies to

In the previous article, we looked at different methods to generate a private key. Whatever method you choose, you’ll end up with 32 bytes of data. Here’s the one that we got at the end of that article:

60cf347dbc59d31c1358c8e5cf5e45b822ab85b79cb32a9f3d98184779a9efc2

We’ll use this private key throughout the article to derive both a public key and the address for the Bitcoin wallet.

What we want to do is to apply a series of conversions to the private key to get a public key and then a wallet address. Most of these conversions are called hash functions. These hash functions are one-way conversions that can’t be reversed. We won’t go to the mechanics of the functions themselves — there are plenty of great articles that cover that. Instead, we will look at how using these functions in the correct order can lead you to the Bitcoin wallet address that you can use.

Elliptic Curve Cryptography

The first thing we need to do is to apply the ECDSA or Elliptic Curve Digital Signature Algorithm to our private key. An elliptic curve is a curve defined by the equation y² = x³ + ax + b with a chosen a and b. There is a whole family of such curves that are widely known and used. Bitcoin uses the secp256k1 curve. If you want to learn more about Elliptic Curve Cryptography, I’ll refer you to this article.

By applying the ECDSA to the private key, we get a 64-byte integer. This consists of two 32-byte integers that represent the X and Y of the point on the elliptic curve, concatenated together.

For our example, we got: 1e7bcc70c72770dbb72fea022e8a6d07f814d2ebe4de9ae3f7af75bf706902a7b73ff919898c836396a6b0c96812c3213b99372050853bd1678da0ead14487d7.

In Python, it would look like this:

Note: as you can see from the code, before I used a method from the ecdsa module, I decoded the private key using codecs. This is relevant more to the Python and less to the algorithm itself, but I will explain what are we doing here to remove possible confusion.

In Python, there are at least two classes that can keep the private and public keys: “str” and “bytes”. The first is a string and the second is a byte array. Cryptographic methods in Python work with a “bytes” class, taking it as input and returning it as the result.

Vmware workstation 12 pro key generator. Now, there’s a little catch: a string, say, 4f3c does not equal the byte array 4f3c, it equals the byte array with two elements, O&lt;. And that’s what codecs.decode method does: it converts a string into a byte array. That will be the same for all cryptographic manipulations that we’ll do in this article.

Public key

Once we’re done with the ECDSA, all we need to do is to add the bytes 0x04 at the start of our public key. The result is a Bitcoin full public key, which is equal to: 041e7bcc70c72770dbb72fea022e8a6d07f814d2ebe4de9ae3f7af75bf706902a7b73ff919898c836396a6b0c96812c3213b99372050853bd1678da0ead14487d7 for us.

Compressed public key

But we can do better. As you might remember, the public key is some point (X, Y) on the curve. We know the curve, and for each X there are only two Ys that define the point which lies on that curve. So why keep Y? Instead, let’s keep X and the sign of Y. Later, we can derive Y from that if needed.

The specifics are as follows: we take X from the ECDSA public key. Now, we add the 0x02 if the last byte of Y is even, and the byte 0x03 if the last byte is odd.

In our case, the last byte is odd, so we add 0x03 to get the compressed public key: 031e7bcc70c72770dbb72fea022e8a6d07f814d2ebe4de9ae3f7af75bf706902a7. This key contains the same information, but it’s almost twice as short as the uncompressed key. Cool!

Diablo 3 game key generator 2015. Previously, wallet software used long, full versions of public keys, but now most of it has switched to compressed keys.

Encrypting the public key

From now on, we need to make a wallet address. Whatever method of getting the public key you choose, it goes through the same procedure. Obviously, the addresses will differ. In this article, we will go with the compressed version.

What we need to do here is to apply SHA-256 to the public key, and then apply RIPEMD-160 to the result. The order is important.

SHA-256 and RIPEMD-160 are two hash functions, and again, we won’t go into the details of how they work. What matters is that now we have 160-bit integer, which will be used for further modifications. Let’s call that an encrypted public key. For our example, the encrypted public key is 453233600a96384bb8d73d400984117ac84d7e8b.

Here’s how we encrypt the public key in Python:

Adding the network byte

The Bitcoin has two networks, main and test. The main network is the network that all people use to transfer the coins. The test network was created — you guessed it — to test new features and software.

We want to generate an address to use it on the mainnet, so we need to add 0x00 bytes to the encrypted public key. The result is 00453233600a96384bb8d73d400984117ac84d7e8b. For the testnet, that would be 0x6f bytes.

Checksum

Now we need to calculate the checksum of our mainnet key. The idea of checksum is to make sure that the data (in our case, the key) wasn’t corrupted during transmission. The wallet software should look at the checksum and mark the address as invalid if the checksum mismatches.

To calculate the checksum of the key, we need to apply SHA-256 twice and then take first 4 bytes of the result. For our example, the double SHA-256 is 512f43c48517a75e58a7ec4c554ecd1a8f9603c891b46325006abf39c5c6b995 and therefore the checksum is 512f43c4 (note that 4 bytes is 8 hex digits).

The code to calculate an address checksum is the following:

Getting the address

Finally, to make an address, we just concatenate the mainnet key and the checksum. That makes it 00453233600a96384bb8d73d400984117ac84d7e8b512f43c4 for our example.

That’s it! That’s the wallet address for the private key at the start of the article.

But you may notice that something is off. You’ve probably seen a handful of Bitcoin addresses and they didn’t look like that. Well, the reason is that they are encoded with Base58. It’s a little bit odd.

Here’s the algorithm to convert a hex address to the Base58 address:

Generate Rsa Public Key

What we get is 17JsmEygbbEUEpvt4PFtYaTeSqfb9ki1F1, a compressed Bitcoin wallet address.

Conclusion

The wallet key generation process can be split into four steps:

• creating a public key with ECDSA
• encrypting the key with SHA-256 and RIPEMD-160
• calculating the checksum with double SHA-256
• encoding the key with Base58.

Depending on the form of public key (full or compressed), we get different addresses, but both are perfectly valid.

Here’s the full algorithm for the uncompressed public key:

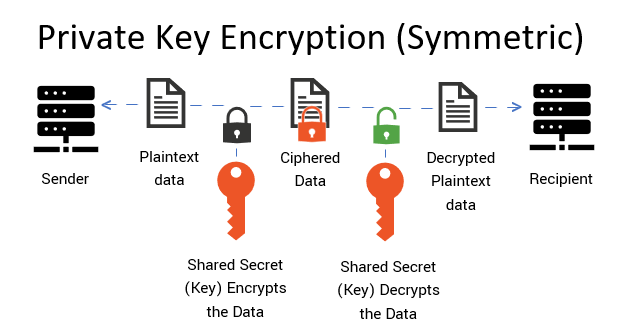
Private Key Encryption

If you want to play with the code, I published it to the Github repository.

I am making a course on cryptocurrencies here on freeCodeCamp News. The first part is a detailed description of the blockchain.

Private Key Definition

I also post random thoughts about crypto on Twitter, so you might want to check it out.