Elliptic Curve Key Generation Example
 -->
-->Jul 26, 2018 For an Elliptic Curve we generate a 256-bit random number for the private key (p), and then take a point (G) x,y on the Elliptic Curve and then multiply it by the private key to get another. Oct 04, 2018 Elliptic Curve Cryptography, or ECC, is a powerful approach to cryptography and an alternative method from the well known RSA. It is an approach used for public key encryption by utilizing the mathematics behind elliptic curves in order to generate security between key pairs. Mar 10, 2014 Key pair generation in elliptic curve follows the same principles as the other algorithms, the main difference being that, unlike algorithms such as RSA, elliptic curve keys exist only in the context of a particular elliptic curve and require to have curve parameters associated with them to be of any use. Jun 26, 2019 Elliptic Curve Addition Operations. Elliptic curves have a few necessary peculiarities when it comes to addition. Two points on the curve (P, Q) will intercept the curve at a third point on the curve. When that point is reflected across the horizontal axis, it becomes the point (R). The primary benefit promised by elliptic curve cryptography is a smaller key size, reducing storage and transmission requirements, i.e. That an elliptic curve group could provide the same level of security afforded by an RSA -based system with a large modulus and correspondingly larger key: for example, a 256-bit elliptic curve public key should provide comparable security to a 3072-bit RSA public key. Oct 24, 2013 CloudFlare uses elliptic curve cryptography to provide perfect forward secrecy which is essential for online privacy. First generation cryptographic algorithms like RSA and Diffie-Hellman are still the norm in most arenas, but elliptic curve cryptography is quickly becoming the go-to solution for privacy and security online. The public keys are part of the key pair generation by each one of the parties, usually denoted. With ECC the keys can be generated from the private key at any time, as the public key is generated after the private key within the function, namely by multiplying the private key value with the base point.
Elliptic Curve Key Generation Example For Kids
Definition
Provides an abstract base class that encapsulates the Elliptic Curve Digital Signature Algorithm (ECDSA).
- Derived
Remarks
This class serves as the abstract base class for ECDsaCng derivations.
Constructors
| ECDsa() | Initializes a new instance of the ECDsa class. |
Fields
| KeySizeValue | Represents the size, in bits, of the key modulus used by the asymmetric algorithm. (Inherited from AsymmetricAlgorithm) |
| LegalKeySizesValue | Specifies the key sizes that are supported by the asymmetric algorithm. (Inherited from AsymmetricAlgorithm) |
Properties
| KeyExchangeAlgorithm | Gets the name of the key exchange algorithm. |
| KeySize | Gets or sets the size, in bits, of the key modulus used by the asymmetric algorithm. (Inherited from AsymmetricAlgorithm) |
| LegalKeySizes | Gets the key sizes that are supported by the asymmetric algorithm. (Inherited from AsymmetricAlgorithm) |
| SignatureAlgorithm | Gets the name of the signature algorithm. |
Methods
| Clear() | Releases all resources used by the AsymmetricAlgorithm class. (Inherited from AsymmetricAlgorithm) |
| Create() | Creates a new instance of the default implementation of the Elliptic Curve Digital Signature Algorithm (ECDSA). |
| Create(ECCurve) | Creates a new instance of the default implementation of the Elliptic Curve Digital Signature Algorithm (ECDSA) with a newly generated key over the specified curve. |
| Create(ECParameters) | Creates a new instance of the default implementation of the Elliptic Curve Digital Signature Algorithm (ECDSA) using the specified parameters as the key. |
| Create(String) | Creates a new instance of the specified implementation of the Elliptic Curve Digital Signature Algorithm (ECDSA). |
| Dispose() | Releases all resources used by the current instance of the AsymmetricAlgorithm class. (Inherited from AsymmetricAlgorithm) |
| Dispose(Boolean) | Releases the unmanaged resources used by the AsymmetricAlgorithm class and optionally releases the managed resources. (Inherited from AsymmetricAlgorithm) |
| Equals(Object) | Determines whether the specified object is equal to the current object. (Inherited from Object) |
| ExportECPrivateKey() | Exports the current key in the ECPrivateKey format. |
| ExportEncryptedPkcs8PrivateKey(ReadOnlySpan<Byte>, PbeParameters) | Exports the current key in the PKCS#8 EncryptedPrivateKeyInfo format with a byte-based password. (Inherited from AsymmetricAlgorithm) |
| ExportEncryptedPkcs8PrivateKey(ReadOnlySpan<Char>, PbeParameters) | Exports the current key in the PKCS#8 EncryptedPrivateKeyInfo format with a char-based password. (Inherited from AsymmetricAlgorithm) |
| ExportExplicitParameters(Boolean) | When overridden in a derived class, exports the explicit parameters for an elliptic curve. |
| ExportParameters(Boolean) | When overridden in a derived class, exports the named or explicit parameters for an elliptic curve. If the curve has a name, the Curve field contains named curve parameters, otherwise it contains explicit parameters. |
| ExportPkcs8PrivateKey() | Exports the current key in the PKCS#8 PrivateKeyInfo format. (Inherited from AsymmetricAlgorithm) |
| ExportSubjectPublicKeyInfo() | Exports the public-key portion of the current key in the X.509 SubjectPublicKeyInfo format. (Inherited from AsymmetricAlgorithm) |
| FromXmlString(String) | This method throws in all cases. |
| GenerateKey(ECCurve) | When overridden in a derived class, generates a new ephemeral public/private key pair for the specified curve, replacing the current key. |
| GetHashCode() | Serves as the default hash function. (Inherited from Object) |
| GetType() | Gets the Type of the current instance. (Inherited from Object) |
| HashData(Byte[], Int32, Int32, HashAlgorithmName) | When overridden in a derived class, computes the hash value of the specified portion of a byte array by using the specified hashing algorithm. |
| HashData(Stream, HashAlgorithmName) | When overridden in a derived class, computes the hash value of the specified binary stream by using the specified hashing algorithm. |
| ImportECPrivateKey(ReadOnlySpan<Byte>, Int32) | Imports the public/private keypair from an ECPrivateKey structure, replacing the keys for this object. |
| ImportEncryptedPkcs8PrivateKey(ReadOnlySpan<Byte>, ReadOnlySpan<Byte>, Int32) | Imports the public/private keypair from a PKCS#8 EncryptedPrivateKeyInfo structure after decrypting with a byte-based password, replacing the keys for this object. |
| ImportEncryptedPkcs8PrivateKey(ReadOnlySpan<Char>, ReadOnlySpan<Byte>, Int32) | Imports the public/private keypair from a PKCS#8 EncryptedPrivateKeyInfo structure after decrypting with a char-based password, replacing the keys for this object. |
| ImportParameters(ECParameters) | When overridden in a derived class, imports the specified parameters. |
| ImportPkcs8PrivateKey(ReadOnlySpan<Byte>, Int32) | Imports the public/private keypair from a PKCS#8 PrivateKeyInfo structure after decryption, replacing the keys for this object. |
| ImportSubjectPublicKeyInfo(ReadOnlySpan<Byte>, Int32) | Imports the public key from an X.509 SubjectPublicKeyInfo structure after decryption, replacing the keys for this object. |
| MemberwiseClone() | Creates a shallow copy of the current Object. (Inherited from Object) |
| SignData(Byte[], HashAlgorithmName) | Computes the hash value of the specified byte array using the specified hash algorithm and signs the resulting hash value. |
| SignData(Byte[], Int32, Int32, HashAlgorithmName) | Computes the hash value of a portion of the specified byte array using the specified hash algorithm and signs the resulting hash value. |
| SignData(Stream, HashAlgorithmName) | Computes the hash value of the specified stream using the specified hash algorithm and signs the resulting hash value. |
| SignHash(Byte[]) | Generates a digital signature for the specified hash value. |
| ToString() | Returns a string that represents the current object. (Inherited from Object) |
| ToXmlString(Boolean) | This method throws in all cases. |
| TryExportECPrivateKey(Span<Byte>, Int32) | Attempts to export the current key in the ECPrivateKey format into a provided buffer. |
| TryExportEncryptedPkcs8PrivateKey(ReadOnlySpan<Byte>, PbeParameters, Span<Byte>, Int32) | Attempts to export the current key in the PKCS#8 EncryptedPrivateKeyInfo format into a provided buffer, using a byte-based password. |
| TryExportEncryptedPkcs8PrivateKey(ReadOnlySpan<Char>, PbeParameters, Span<Byte>, Int32) | Attempts to export the current key in the PKCS#8 EncryptedPrivateKeyInfo format into a provided buffer, using a char-based password. |
| TryExportPkcs8PrivateKey(Span<Byte>, Int32) | Attempts to export the current key in the PKCS#8 PrivateKeyInfo format into a provided buffer. |
| TryExportSubjectPublicKeyInfo(Span<Byte>, Int32) | Attempts to export the current key in the X.509 SubjectPublicKeyInfo format into a provided buffer. |
| TryHashData(ReadOnlySpan<Byte>, Span<Byte>, HashAlgorithmName, Int32) | Attempts to compute the hash value of the specified read-only span of bytes into the provided destination by using the specified hashing algorithm. |
| TrySignData(ReadOnlySpan<Byte>, Span<Byte>, HashAlgorithmName, Int32) | Attempts to compute the ECDSA digital signature for the specified read-only span of bytes into the provided destination by using the specified hashing algorithm and the current key. |
| TrySignHash(ReadOnlySpan<Byte>, Span<Byte>, Int32) | Attempts to compute the ECDSA digital signature for the specified read-only span of bytes representing a data hash into the provided destination by using the current key. |
| VerifyData(Byte[], Byte[], HashAlgorithmName) | Verifies that a digital signature is appropriate for the current key and provided data with a specified hash algorithm. |
| VerifyData(Byte[], Int32, Int32, Byte[], HashAlgorithmName) | Verifies that a digital signature is appropriate for the current key and provided portion of data with a specified hash algorithm. |
| VerifyData(ReadOnlySpan<Byte>, ReadOnlySpan<Byte>, HashAlgorithmName) | Verifies that a digital signature is appropriate for the current key and provided data with a specified hash algorithm. |
| VerifyData(Stream, Byte[], HashAlgorithmName) | Verifies that a digital signature is appropriate for the current key and provided data with a specified hash algorithm. |
| VerifyHash(Byte[], Byte[]) | Verifies that a digital signature is appropriate for the current key and provided data hash. |
| VerifyHash(ReadOnlySpan<Byte>, ReadOnlySpan<Byte>) | Verifies that a digital signature is appropriate for the current key and provided data hash. |
Explicit Interface Implementations
| IDisposable.Dispose() | For a description of this member, see Dispose(). (Inherited from AsymmetricAlgorithm) |
Applies to
- Related Questions & Answers
- Selected Reading
Elliptic curve cryptography is used to implement public key cryptography. It was discovered by Victor Miller of IBM and Neil Koblitz of the University of Washington in the year 1985. ECC popularly used an acronym for Elliptic Curve Cryptography. It is based on the latest mathematics and delivers a relatively more secure foundation than the first generation public key cryptography systems for example RSA.
Elliptic Curves
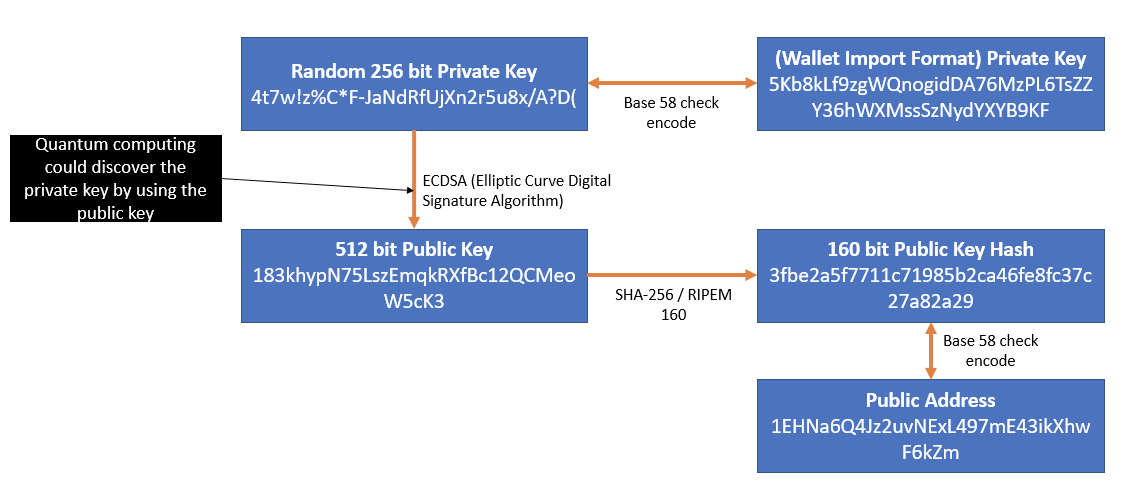
In 1985, cryptographic algorithms were proposed based on elliptic curves. https://intensivedouble.weebly.com/blog/mac-pro-iphoto-editing-software-changed-with-sierra-upgrade. An elliptic curve is the set of points that satisfy a specific mathematical equation. They are symmetrical.
Uses
Websites make extensive use of ECC to secure customers’ hypertext transfer protocol connections.
It is used for encryption by combining the key agreement with a symmetric encryption scheme.
Elliptic Curve Cryptography Example
It is also used in several integer factorization algorithms like Lenstra elliptic-curve factorization.
Time stamping uses an encryption model called a blind signature scheme. It is possible using Elliptic Curve Cryptography.